1004: 子数组4
题目描述
给定一个数组,你需要为每个元素找到包含该元素的最大长度的子数组,其费用至少为$k$。
具体来说,$A$={$A_1,A_2,...,A_n$}是一个长度为$n$的数组,$A_{l...r}$={$A_l,A_{l+1},...,A_r$}是从下标$l$到$r$的子数组,有以下几种相关运算:
$MAX(l,r)$是$A_{l...r}$中最大的数,
$MIN(l,r)$是$A_{l...r}$中最小的数,
$OR(l,r)$是$A_{l...r}$中各元素按位或的结果,
$AND(l,r)$是$A_{l...r}$中各元素按位与的结果。
$A_{l...r}$的费用表示为$cost(l,r)$,定义为:
$cost(l,r)=(OR(l,r)-AND(l,r))-(MAX(l,r)-MIN(l,r))$。
$A_{l...r}$的长度定义为$r-l+1$。
给定一个数组$A$和一个整数$k$,对于每个索引$i(1 \leq i \leq n)$,你的任务是找到最大长度的子数组$A_{l...r}$使得$1 \leq l \leq i \leq r \leq n$且$cost(l,r) \geq k$。
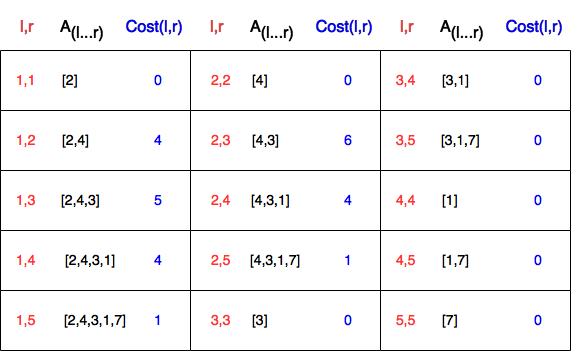
例如,对于数组$A$={$2,4,3,1,7$},$k=6$,可能的子数组及其费用如下:
输入
第一行两个整数,分别表示数组$A$的长度$n$和最低费用$k$。
第二行$n$个整数,表示数组$A$各元素的值。
输出
$n$行,每行一个整数,第$i$行的整数表示数组$A$中包含第$i$个元素的子数组的最大长度,要求其费用至少为$k$,如果不存在这样的子数组则输出$-1$。
样例输入 复制
5 6
2 4 3 1 7样例输出 复制
-1
2
2
-1
-1提示
【样例解释】
对于样例1:
在这个例子中,我们有$k=6$,而只有一个子数组的成本至少为$6$,那就是$A_{2...3}$={$4,6$},$cost(2,3)=6$,它的长度是$2$。因此,对于$i=2$和$i=3$答案是$2$,而对于其它的是$-1$。
【数据范围】
对于5%的数据,$1 \leq n \leq 100$。
对于15%的数据,$1 \leq n \leq 5*10^3$。
对于100%的数据,$1 \leq n \leq 10^5$,$1 \leq A_i \leq 10^9$,$0 \leq k \leq 10^9$。